defringe

Guides & Examples:

• Defringe User Guide
  • Data Setup
  • 1. Normalize the Fringe Flat
  • 2. Prepare the Science File for the Defringing Correction (Optional)
  • 3. Match Fringes in the Fringe Flat Field and the Science Spectra
  • 4. Defringe the Science Spectra
  • Extraction of 1D Spectra from Defringed Science Products
• Defringe Examples
  • G750L Observation of HZ43
  • G750M Observation of AGK+81D266
  • Subarray Data

Table of File Inputs/Outputs for the Defringe Tools

Tool	Input(s)	Output(s)
normspflat	If do_cal is True: [flat_file]_raw.fits, [sci_file]_wav.fits If do_cal is False: [flat_file]_crj.fits (G750L) or [flat_file]_sx2.fits (G750M) [sci_file]_wav.fits	[flat_file]_nsp.fits
prepspec	[sci_file]_raw.fits	Standard Calstis Outputs: [sci_file]_flt.fits [sci_file]_crj.fits [sci_file]_sx1.fits [sci_file]_sx2.fits
mkfringeflat	[flat_file]_nsp.fits [sci_file]_crj.fits (G750L) or [sci_file]_sx2.fits (G750M)	[flat_file]_frr.fits
defringe	[flat_file]_frr.fits [sci_file]_crj.fits (for G750L) or [sci_file]_sx2.fits (for G750M)	[sci_file]_drj.fits (G750L) or [sci_file]_s2d.fits (G750M)

Effectiveness of the Defringing Tools

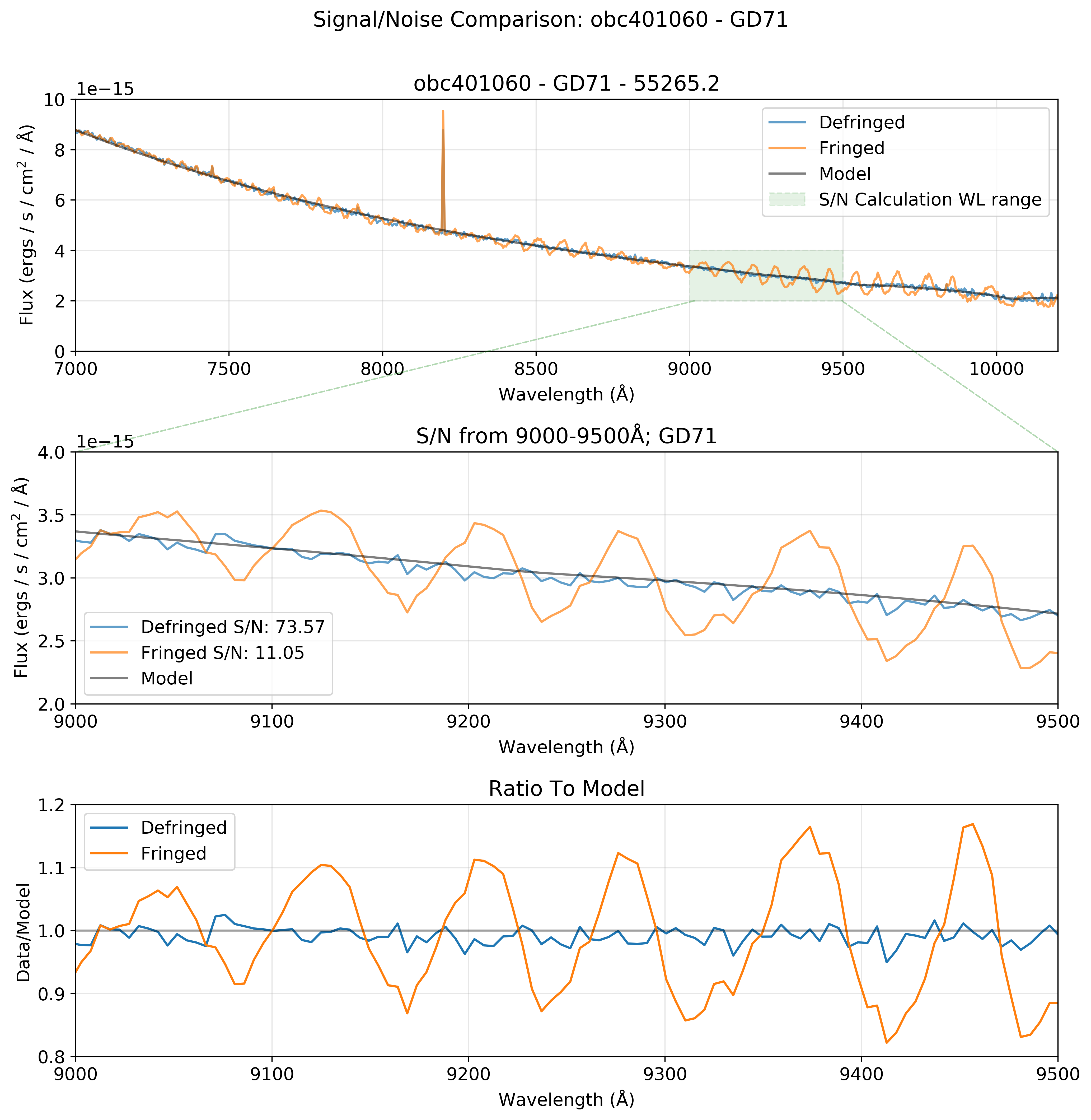
The defringing process has the potential to significantly increase the signal-to-noise ratio of an observation. By removing fringes in an observation of a standard white dwarf target with a well characterized model, we measured an increase in the signal-to-noise ratio from 11 to 73 in the 9000-9500Å wavelength range.

Depending on wavelength range, target, and other observational parameters, we expect that the presence of fringes in an observation may reduce signal-to-noise by up to a factor of 7x. By removing these fringes, we improve the signal-to-noise ratio accordingly.

We calculate the signal-to-noise as 1 divided by the standard deviation of the ratio of the data to the model for a given wavelength range.

Routines

• prepspec — Calibrate STIS CCD G750L or G750M spectrum before defringing

• normspflat — Normalize STIS CCD fringe flat

• mkfringeflat — Match fringes in STIS fringe flat to those in science data

• defringe — Defringe by dividing the science spectrum by the fringe flat

Note

See Section 3.5.5 of the STIS Data Handbook (DHB) for more details on the defringing process.

Warning

These routines are based on PyRAF stsdas.hst_calib.stis defringing tasks, though users should expect numerical discrepancies between these two implementations.

prepspec

stistools.defringe.prepspec(inspec, outroot='./', darkfile=None, pixelflat=None, initguess=None)

Calibrate STIS CCD G750L or G750M spectrum before defringing.

Based on the PyRAF stsdas.hst_calib.stis.prepspec task.

Parameters:

inspec: str

Name of input 'raw' science spectrum

outroot: str

Root for output file name. (Default='./')

darkfile: str or None

Name of superdark image. If None, use DARKFILE in main header of input spectrum.

pixelflat: str or None

Name of pixel-to-pixel flat. If None, use PIXELFLAT in main header of input spectrum.

initguess: str or None

Method for initial value estimate for ocrreject: {None, 'minimum', 'median'}. (Default=None; Use the value in the CRREJTAB.)

Returns:

outname: str

Fully qualified name of prepared spectrum (CRJ or SX2 file)

normspflat

stistools.defringe.normspflat(inflat, outflat='.', do_cal=True, biasfile=None, darkfile=None, pixelflat=None, wavecal=None)

Normalize STIS CCD fringe flat.

Based on the PyRAF stsdas.hst_calib.stis.normspflat task.

Parameters:

inflat: str

Name of input fringe flat

outflat: str

Name of normalized fringe flat output or directory location. (Default=".")

do_cal: bool

Perform bias and dark subtraction and CR rejection? (Default=True)

biasfile: str or None

Name of superbias image. If None, use BIASFILE in main header of the inflat.

darkfile: str or None

Name of superdark image. If None, use DARKFILE in main header of the inflat.

pixelflat: str or None

Name of pixel-to-pixel flat. If None, use PFLTFILE in main header of the inflat.

wavecal: str or None

Name of wavecal file [ONLY FOR G750M SPECTRA]. If None, use WAVECAL in main header of the inflat.

Returns:

outname: str

Fully qualified name of the outflat

mkfringeflat

stistools.defringe.mkfringeflat(inspec, inflat, outflat, do_shift=True, beg_shift=-0.5, end_shift=0.5, shift_step=0.1, do_scale=True, beg_scale=0.8, end_scale=1.2, scale_step=0.04, extrloc=None, extrsize=None, opti_spreg=None, rms_region=None)

Takes an input science spectrum and a fringe flat that has been normalized using the task normspflat. The fringe flat is shifted and scaled to produce the minimum RMS when divided into the science data.

Based on the PyRAF stsdas.hst_calib.stis.mkfringeflat task.

In mkfringeflat, the user can specify a range of shifts and scales for the routine to test creating an optimal fringe flat. mkfringeflat will go through the shift and scale dimensions separately and calculate the RMS using the following steps:

1. For each shift step, apply the shift to the input flat field

2. Divide the science data by the shifted flat

3. Divide out the large-scale SED from the science image using a spline fit in order to isolate the fringing pattern (this is called the response image)

4. Sum the response image along the columns within the RMS region

5. Calculate the mean and standard deviation of the summed columns of the response image

6. The RMS value for that shift is given by the standard deviation divided by the mean found in step 5

7. Fit the RMS values with a quadratic polynomial weighted by the inverse RMS to find the optimal RMS value

8. Apply the best shift determined in step 7 to the data and repeat steps 1-7 with the scale values to find the best scaling

The RMS values are printed out for each scale and shift but the final best shift and best scale values do not necessarily correspond to the printed values. This is because the routine is calculating the RMS values based on a fit of the data at each scale and shift, rather than being calculated at each discrete step.

Parameters:

inspec: str

Name of input science spectrum datafile

inflat: str

Name of input fringe flat file (usually the output from normspflat)

outflat: str

Name of output fringe flat to be used in the defringe task

do_shift: bool

Controls whether the shift between fringe flat and science data is to be calculated

beg_shift: float

Initial shift to apply to fringe flat

end_shift: float

Final shift to apply to fringe flat

shift_step: float

Step-size between shifts to be applied to fringe flat

do_scale: bool

Controls whether the scaling between fringe flat and science data is to be calculated

beg_scale: float

Initial scaling to apply to fringe flat

end_scale: float

Final scaling to appply to fringe flat

scale_step: float

Step-size between scaling values to be applied to fringe flat

extrloc: float or None

Extraction location. If set to None, this will be calculated by parabolic interpolation of the peak of the cross-dispersion spectral sum

extrsize: float or None

Extraction size in pixels. If set to None, this will be set to a reasonable value by this routine

opti_spreg: list or array-like or None

A list or array representing the section to be used in normalizing the spectrum of the science target before it is divided by the shifted/scaled fringe flat. If set to None, a reasonable range is chosen by this routine. Should be specified like a Python slice, zero indexed.

rms_region: list or array-like or None

A list or array representing the section to be used in the rms calculation. If set to None, a reasonable range is chosen by this routine. Should be specified like a Python slice, zero indexed.

defringe

stistools.defringe.defringe(science_file, fringe_flat, overwrite=True, verbose=True)

Defringe by dividing the science spectrum by the fringe flat.

Based on the PyRAF stsdas.hst_calib.stis.defringe task.

Parameters:

science_file: str

The name of the input science file.

fringe_flat: str

The name of the input fringe flat file. This is the output from mkfringeflat.

overwrite: bool

The name of the output file will be constructed from the name of the input science file (science_file) by replacing the suffix with 'drj' or 's2d'. If the input name are the same a RuntimeError will be raised, rather than modifying the input in-place. If there is an existing file with the same name as the output name, the existing file will be overwritten if overwrite is True (the default is True).

verbose: bool

If True (the default), print more info.

Returns:

drj_filename: str

The name of the output file. This will have suffix '_drj' if the input is G750L data, and the output name will have suffix '_s2d' if the input is G750M.